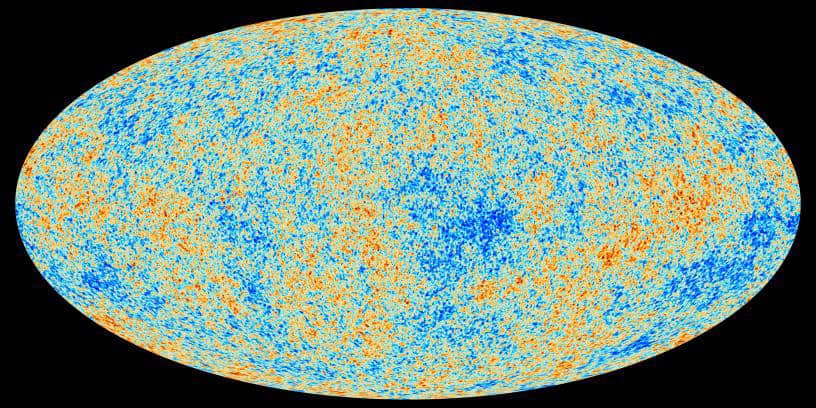
Loop quantum cosmology may explain smoothness of cosmic microwave background

 

Loop quantum cosmology may explain the smoothness of the cosmic microwave background

09 May 2025 Sponsored by EPL

Repulsive gravity at the quantum scale would have flattened out inhomogeneities in the early universe

First light: The cosmic microwave background, as imaged by the European Space Agency’s Planck mission. (Courtesy: ESA and the Planck Collaboration)

In classical physics, gravity is universally attractive. At the quantum level, however, this may not always be the case. If vast quantities of matter are present within an infinitesimally small volume – at the centre of a black hole, for example, or during the very earliest moments of the universe – spacetime becomes curved at scales that approach the Planck length. This is the fundamental quantum unit of distance, and is around 1020 times smaller than a proton.

In these extremely curved regions, the classical theory of gravity – Einstein’s general theory of relativity – breaks down. However, research on loop quantum cosmology offers a possible solution. It suggests that gravity, in effect, becomes repulsive. Consequently, loop quantum cosmology predicts that our present universe began in a so-called “cosmic bounce”, rather than the Big Bang singularity predicted by general relativity.

In a recent paper published in EPL, Edward Wilson-Ewing, a mathematical physicist at the University of New Brunswick, Canada, explores the interplay between loop quantum cosmology and a phenomenon sometimes described as “the echo of the Big Bang”: the cosmic microwave background (CMB). This background radiation pervades the entire visible universe, and it stems from the moment the universe became cool enough for neutral atoms to form. At this point, light could suddenly travel through space without being continually scattered by the plasma of electrons and light nuclei that existed before. This freshly liberated light makes up the CMB, so studying it offers clues to the early universe. Cosmologist Edward Wilson-Ewing uses loop quantum gravity to study quantum effects in the very early universe. (Courtesy: University of New Brunswick)

What was the motivation for your research?

Observations of the CMB show that the early universe (that is, the universe as it was when the CMB formed) was extremely homogeneous, with relative anisotropies of the order of one part in 104. Classical general relativity has trouble explaining this homogeneity on its own, because a purely attractive version of gravity tends to drive things in the opposite direction. This is because if a region has a higher density than the surrounding area, then according to general relativity, that region will become even denser; there is more mass in that region and therefore particles surrounding it will be attracted to it. Indeed, this is how the small inhomogeneities we do see in the CMB grew over time to form stars and galaxies today.

The main way this gets resolved in classical general relativity is to suggest that the universe experienced an episode of super-rapid growth in its earliest moments. This super-rapid growth is known as inflation, and it can suffice to generate homogeneous regions. However, in general, this requires a very large amount of inflation (much more than is typically considered in most models).

Alternately, if for some reason there happens to be a region that is moderately homogeneous when inflation starts, this region will increase exponentially in size while also becoming further homogenized. This second possibility requires a little more than a minimal amount of inflation, but not much more.

My goal in this work was to explore whether, if gravity becomes repulsive in the deep quantum regime (as is the case in loop quantum cosmology), this will tend to dilute regions of higher density, leading to inhomogeneities being smoothed out. In other words, one of the main objectives of this work was to find out whether quantum gravity could be the source of the high degree of homogeneity observed in the CMB.

What did you do in the paper?

In this paper, I studied spherically symmetric spacetimes coupled to dust (a simple model for matter) in loop quantum cosmology. These spacetimes are known as Lemaître-Tolman-Bondi spacetimes, and they allow arbitrarily large inhomogeneities in the radial direction. They therefore provide an ideal arena to explore whether homogenization can occur: they are simple enough to be mathematically tractable, while still allowing for large inhomogeneities (which, in general, are very hard to handle).

Loop quantum cosmology predicts several leading-order quantum effects. One of these effects is that spacetime, at the quantum level, is discrete: there are quanta of geometry just as there are quanta of matter. This has implications for the equations of motion, which relate the geometry of spacetime to the matter in it. If we consider the discrete nature of quantum geometry, we must modify the equations of motion.

These modifications are captured by so-called effective equations, and in the paper, I solved these equations numerically for a wide range of initial conditions. From this, I found that while homogenization doesn’t occur everywhere, it always happens in some regions. These homogenized regions can then be blown up to cosmological scales by inflation (and inflation will further homogenize them). Therefore, this quantum gravity homogenization process could indeed explain the homogeneity observed in the CMB.

What do you plan to do next?

Extending this work in several directions is important to check the robustness of the homogenization effect in loop quantum cosmology. The restriction to spherical symmetry should be relaxed, although this will be challenging from a mathematical perspective. It will also be important to go beyond dust as a description of matter. The simplicity of dust makes calculations easier, but it is not particularly realistic.

Other relevant forms of matter include radiation and the so-called inflaton field, which is a type of matter that can cause inflation to occur. That said, in cosmology, physics is somewhat independent of the universe’s matter content, at least at a qualitative level. Different types of matter content may dilute more rapidly than others in an expanding universe. The universe may expand at different rates depending on its matter content. The main properties of the cosmological dynamics (for example, the expanding universe, the occurrence of an initial singularity, and so on) within general relativity are independent of the specific matter being considered.

Therefore, it is reasonable to expect that the quantitative predictions will depend on the matter content. Still, the qualitative features (in particular, that small regions are homogenized by quantum gravity) will remain the same. Further research is needed to test this expectation.

FROM PHYSICSWORLD.COM     12-05-2025