Quantum complexity could solve a wormhole paradox

03 May 2022 Campbell McLauchlan

Boundary issue: Finding the dual quantity to wormhole volume under the holographic principle is a key outstanding problem in quantum gravity. (Courtesy: AllenMcC., CC BY-SA 3.0 <https://creativecommons.org/licenses/by-sa/3.0>, via Wikimedia Commons)

Physicists in Germany and the US have proved that the quantum complexity of random circuits grows linearly for extremely long times. The result has implications for the so-called “wormhole growth paradox” in theories of quantum gravity thanks to a proposed link between complexity and the volume of wormholes – hypothesized shortcuts connecting far-separated regions of space in Einstein’s general theory of relativity.

Finding a quantum theory of gravity is one of the most famous problems in physics, and the holographic principle offers an intriguing route to solving it. The idea is to try to describe quantum gravity within a patch of space by focusing on the boundary of that patch, which is described by a non-gravitational theory. Any quantity in the gravitational theory that applies to the bulk of the patch should be equivalent or “dual” to some other quantity in the theory that applies to the boundary.

However, a paradox arises when introducing wormholes into space–time. Known as the “wormhole growth paradox”, it occurs because while the volume of a wormhole grows for a very long time (depending exponentially on the size of the patch), the boundary seems to settle into equilibrium much more quickly. Hence, determining the dual quantity of the ever-expanding wormhole volume is an important challenge.

A complex key

The wormhole growth paradox was first identified by the American physicist Leonard Susskind in 2014. At the time, Susskind also proposed a solution, suggesting that the “quantum complexity” of the boundary’s state could be dual to the wormhole’s volume. A state’s quantum complexity, roughly speaking, is a measure of how difficult it is to produce that state from an initial reference state. Many theorists in the field believe that quantum complexity continues to grow even after other quantities settle at their equilibrium values, hinting that it could be the key to resolving the paradox.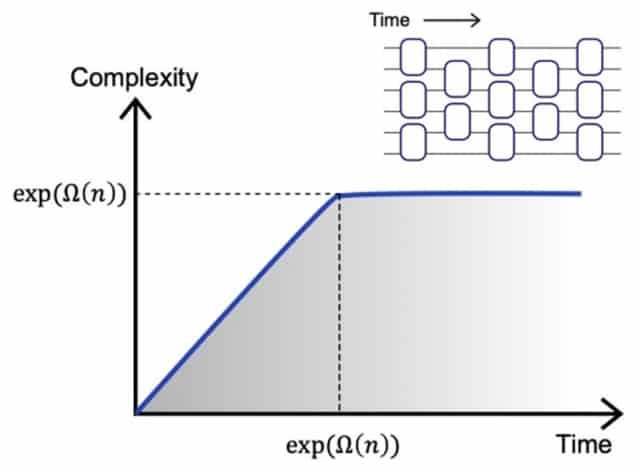Growing complexity: The new result proves that random quantum circuits on n qubits have a complexity that grows linearly for exponentially long times, after which it remains constant. Ω(n) indicates a function that grows at least as quickly as n, for large n. Inset: The team considered quantum circuits formed from random operations (boxes) acting on qubits (lines). (Courtesy: Adapted from J Haferkamp et al. Nat. Phys. https://doi.org/10.1038/s41567-022-01539-6)

Importantly, however, it remained to be proved that the quantum complexity of the boundary state grows in the same way as the wormhole volume in the bulk. In a recent paper in Nature Physics, Jonas Haferkamp, Philippe Faist, Naga Kothakonda, and Jens Eisert from the Freie Universität Berlin and Nicole Yunger Halpern from the University of Maryland showed that it does – at least for a particular class of models.

The researchers considered a very simple quantum system in which two-level quantum bits, or qubits, undergo a series of random, two-qubit transformations. They showed that the quantum complexity of the qubits’ state grew linearly in time until it reached a saturation value at some very late time that depended exponentially on the number of qubits. This pattern precisely mirrors the way in which wormhole volume grows.

The complicating factor in the work is that quantum complexity – which in this case is the minimum number of two-qubit operations that must be performed to arrive at a particular state – is notoriously hard to assess. In fact, it is almost impossible to know whether there is a shortcut to producing the same state with fewer operations.

Proxy considerations

The researchers found a way around this by considering a proxy quantity instead: the dimension of the space of all possible states the system could reach by performing N two-qubit operations. If they could show that this “accessible dimension” increased with each operation, that would amount to proving that the overwhelming majority of these states cannot be reached by fewer than N operations. Thus, randomly performing operations on an initial state generically produces states with a complexity that increases with each operation.

A surprisingly simple class of operations, the so-called Clifford unitaries, provided a key to the proof. “Clifford unitaries are ubiquitous in quantum information,” Haferkamp explains, “but this application was still surprising to me as [despite the complexity of the states being dealt with] Clifford unitaries themselves have very low circuit complexity.” Using this tool, he and his colleagues showed that the accessible dimension – and hence the quantum complexity – increases with each operation, until it reaches its maximum value after an exponentially long time. “One cannot cheat nature,” Haferkamp summarizes. “Long time evolutions cannot be reversed in a substantially shorter time; there are no ‘short-cuts’.”READ MORE

Decoding the quantum horizon

While the new study is the first to demonstrate linear growth of quantum complexity for random qubit circuits, the notion of quantum complexity that Haferkamp and colleagues used is somewhat less general than that considered in a seminal 2016 paper by Fernando Brandão and colleagues. The current theorem is thus stronger in some ways than this previous result and weaker in others. However, random quantum circuits are simply toy models for the boundary states appearing in examples of the holographic principle – those that could shed some light on quantum gravity – and other fruitful approaches are being pursued in parallel. Hence, these results are an important but preliminary step towards solving the wormhole growth paradox. In Haferkamp’s words, the team’s work provides a crucial “sanity check” for the proposed solution to the paradox, namely that volume is equivalent to complexity.

from physicsworld.com    8/5/2022