Real-world quantum entanglement is far from an unlimited resource

19 Dec 2025 Daniele Iannotti 

Different approaches: Two entities, traditionally known as Alice and Bob, can manipulate the quantum states held at their respective laboratories using only local operations and classical communications (LOCC). The picture illustrates the primary distinction between information-theoretic (1) and computational (2) versions of entanglement manipulation. (Courtesy: Leone, L, Rizzo, J, Eisert, J et al. Entanglement theory with limited computational resources. Nat. Phys. 21, 1847–1854 (2025). https://doi.org/10.1038/ CC-BY-4.0 http://creativecommons.org/licenses/by/4.0/.s41567-025-03048-8)

Achieving a profound understanding of any subject is hard. When that subject is quantum mechanics, it’s even harder. And when one departs from ideal theoretical scenarios and enters the real world of experimental limitations, it becomes more challenging still – yet that is what physicists at the Freie Universität Berlin (FU-Berlin), Germany, recently did by exploring what happens to entanglement theory in real quantum computers. In doing so, they created a bridge between two fields that have so far developed mainly in parallel: entanglement theory (rooted in physics) and computational complexity (rooted in computer science).

Ebits, the standard currency of entanglement

In quantum mechanics, a composite system is said to be entangled when its total wavefunction cannot be written as a product of the states of its individual subsystems. This leads to correlations between subsystems that arise from the structure of the quantum state, not from any shared classical information. Many speedups achieved in quantum computing, quantum cryptography, and quantum metrology rely heavily on entanglement, but not all forms of entanglement are equally helpful. Only specific kinds of entanglement will enable a given computational or communication task.

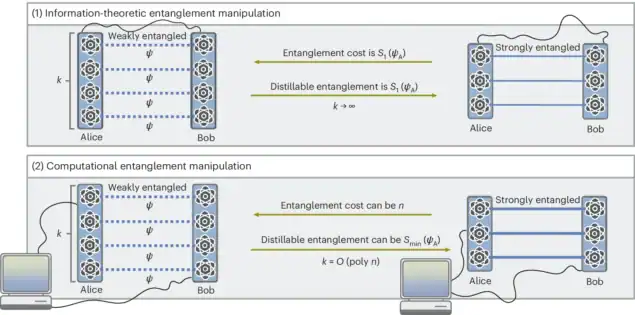
To make quantum technologies practical, the available entangled resources must therefore often be converted into forms suitable for specific applications. One primary conversion process involves transforming partially entangled states into, or extracting them from, the maximally entangled bit (ebit), which serves as the standard unit of entanglement. High-fidelity ebits – entangled pairs that are incredibly close to the ideal perfectly entangled state – can be distilled from noisy or imperfect entangled states through entanglement distillation. In contrast, entanglement dilution enables reconstruction of the desired entangled states from purified EPRBs.

In an idealized setting, with an infinite number of copies of entangled states and unlimited computational power, a single quantity called the von Neumann entropy fully determines how many ebits can be extracted or are required. But reality is far less forgiving: we never have infinite resources, and computational power is always limited, just like we don’t have an endless amount of gold on Earth.

Entanglement under finite resources

In the present work, published in Nature Physics, the FU-Berlin team of Lorenzo Leone, Jacopo Rizzo, Jens Eisert, and Sofiene Jerbi investigated what happens when these ideal assumptions break down. They study the case in which only a finite number of entangled states, which scale at most polynomially with the number of quantum bits (qubits) in the system, are considered, and all local operations and classical communication (LOCC) are performed in finite polynomial time.

They found that the simple correspondence between von Neumann entropy and extractable or required ebits no longer holds: even when a state has a large von Neumann entropy, the number of ebits that can be efficiently extracted may be much lower. In these cases, the number is bounded instead by the min-entropy of the reduced state (an operational measure determined solely by the state’s largest eigenvalue that captures how much entanglement can be reliably distilled from a single copy of the state) without averaging over many uses. On the other hand, even a state with negligible von Neumann entanglement may require a maximal EBIT budget for efficient dilution.

Leone and Eisert report that they were inspired to conduct this study by recent work on so-called pseudo-entangled states, which appear highly entangled to computationally bounded observers. Their construction of pseudo-entangled states highlights a worst-case scenario: a state that appears almost unentangled by conventional measures may still require a large number of ebits to be created efficiently. The takeaway is that computability matters, and quantum resources you might have thought were available may be locked away simply because they cannot be processed efficiently. In other words, practical limitations make the line between a “resource” and a “usable resource” even sharper.

Quantum resources in a limited world

The researchers say that their study raises multiple questions for future exploration. One such question concerns whether a similar computational‐efficiency gap exists for other quantum resources, such as magic and coherence. Another is whether one can develop a complete resource theory with complexity constraints, in which quantities reflect not only what can be converted but also how efficiently that conversion occurs.

Distillation method strengthens quantum entanglement in a single pair of photons

Regardless of the answers, the era of entanglement under infinite bookkeeping is giving way to an era of entanglement under limited books, limited clocks, and limited gates. In this more realistic space, quantum technologies may still prove effective, but the calculus of what can be done and what can be harnessed requires a substantial retooling.

Daniele Iannotti is a PhD student and contributor to Physics World. Daniele is conducting research in quantum gravity and quantum information at the Scuola Superiore Meridionale (SSM), Italy. Find out more about our student contributor networks. Back to Quantum

from physicsworld.com       25/12/2025